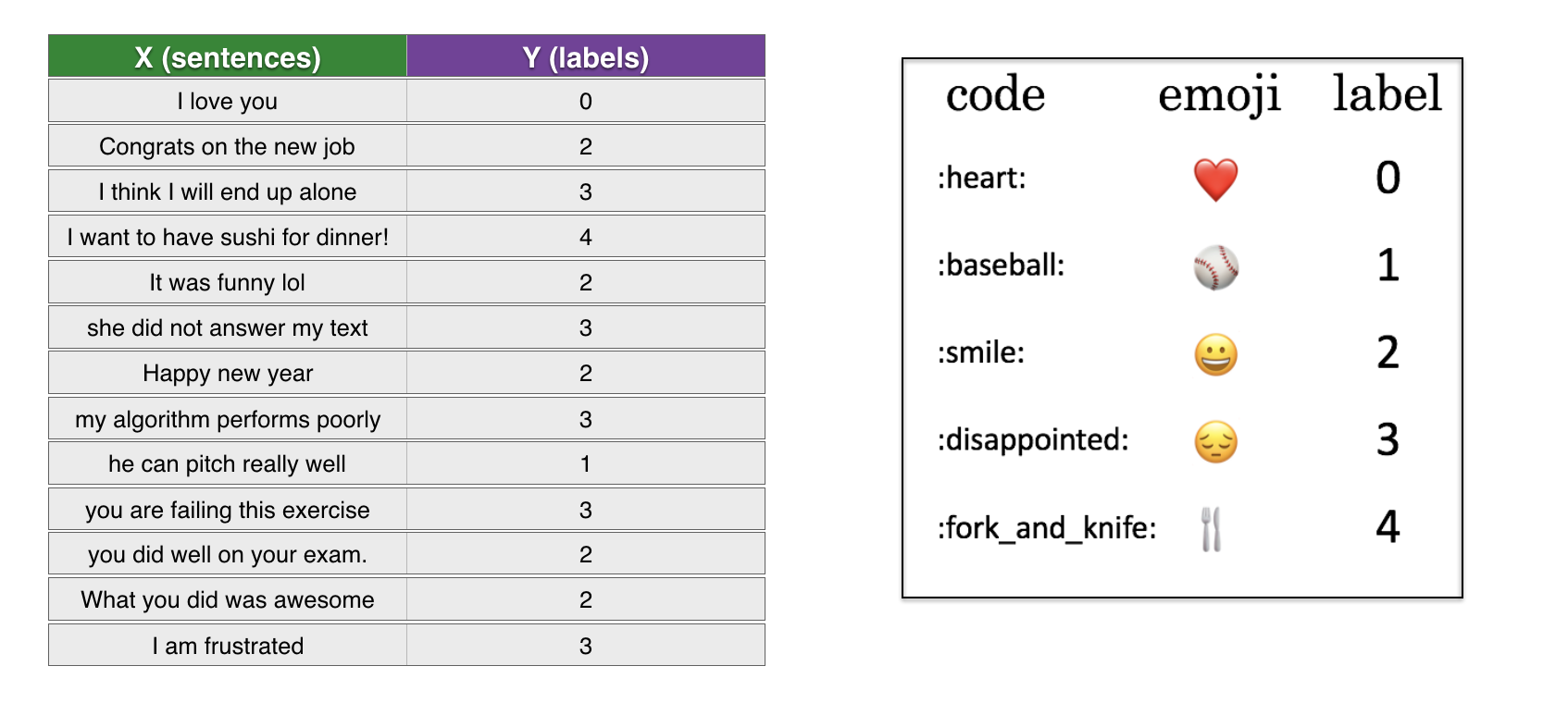
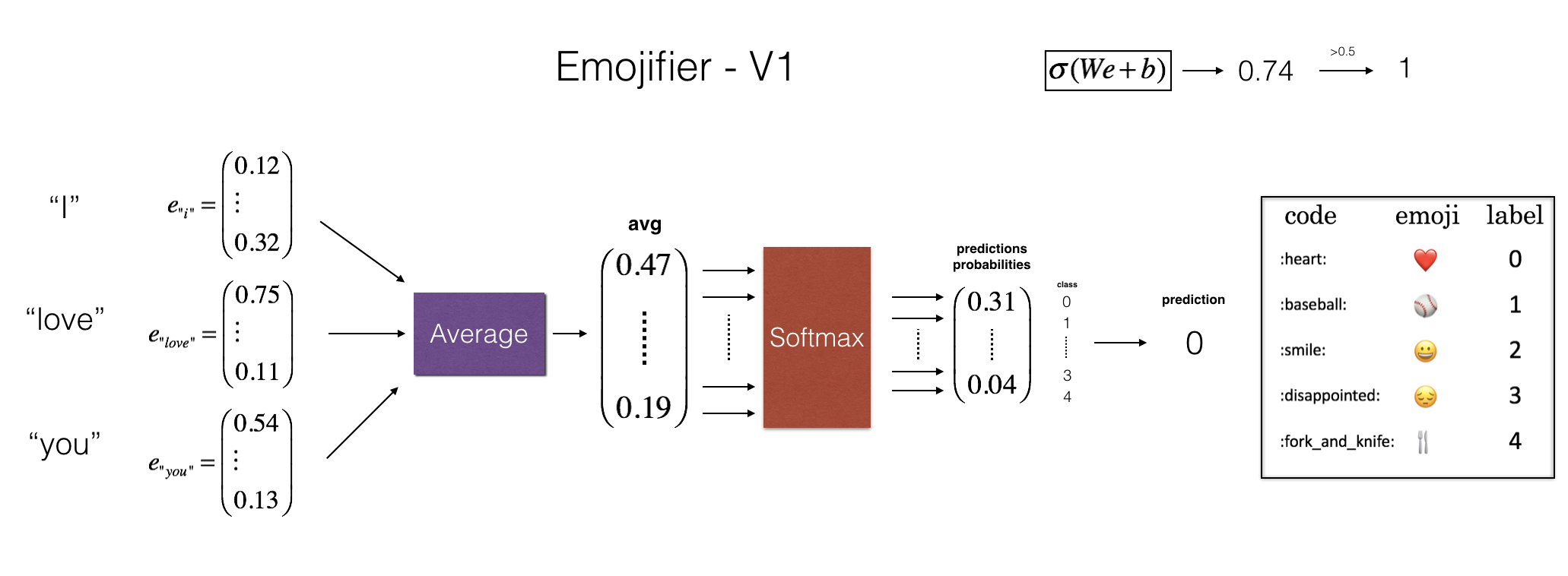
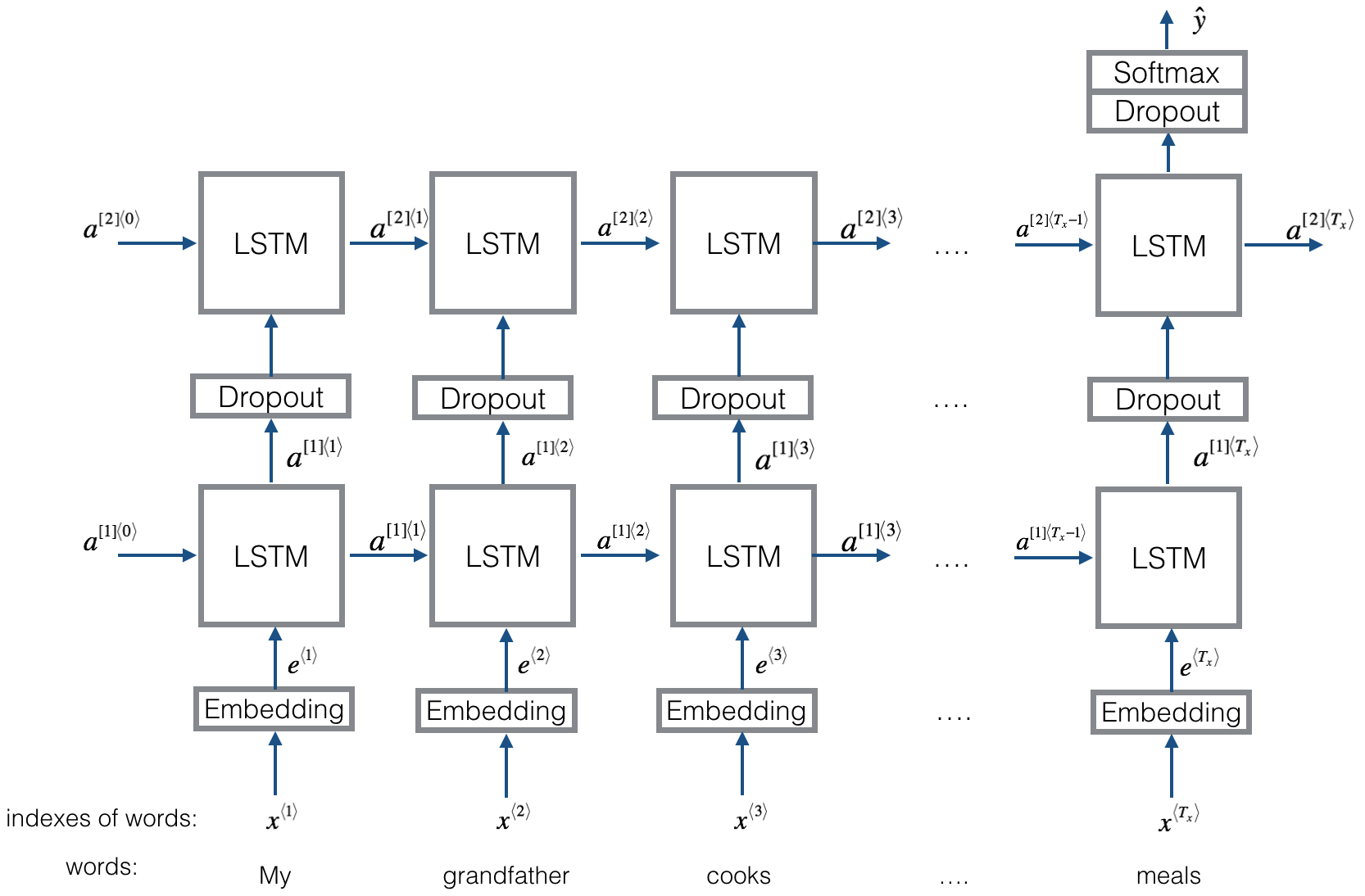
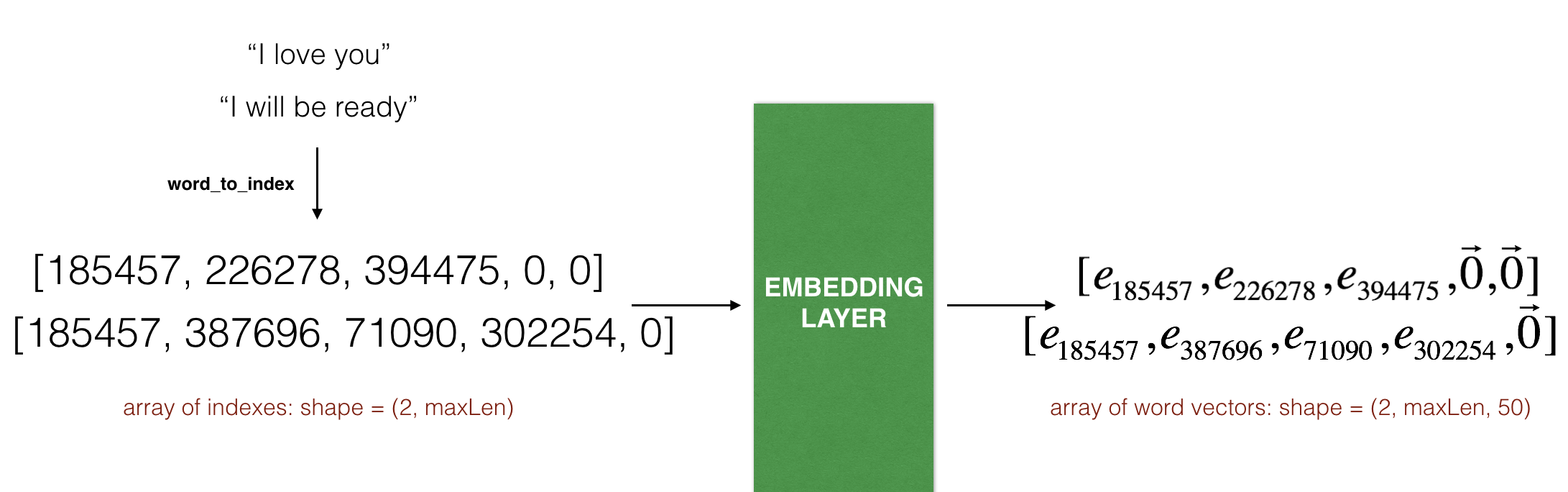
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 10) 0
_________________________________________________________________
embedding_6 (Embedding) (None, 10, 50) 20000050
_________________________________________________________________
lstm_1 (LSTM) (None, 10, 128) 91648
_________________________________________________________________
dropout_1 (Dropout) (None, 10, 128) 0
_________________________________________________________________
lstm_2 (LSTM) (None, 128) 131584
_________________________________________________________________
dropout_2 (Dropout) (None, 128) 0
_________________________________________________________________
dense_1 (Dense) (None, 5) 645
_________________________________________________________________
activation_1 (Activation) (None, 5) 0
=================================================================
Total params: 20,223,927
Trainable params: 223,877
Non-trainable params: 20,000,050
_________________________________________________________________