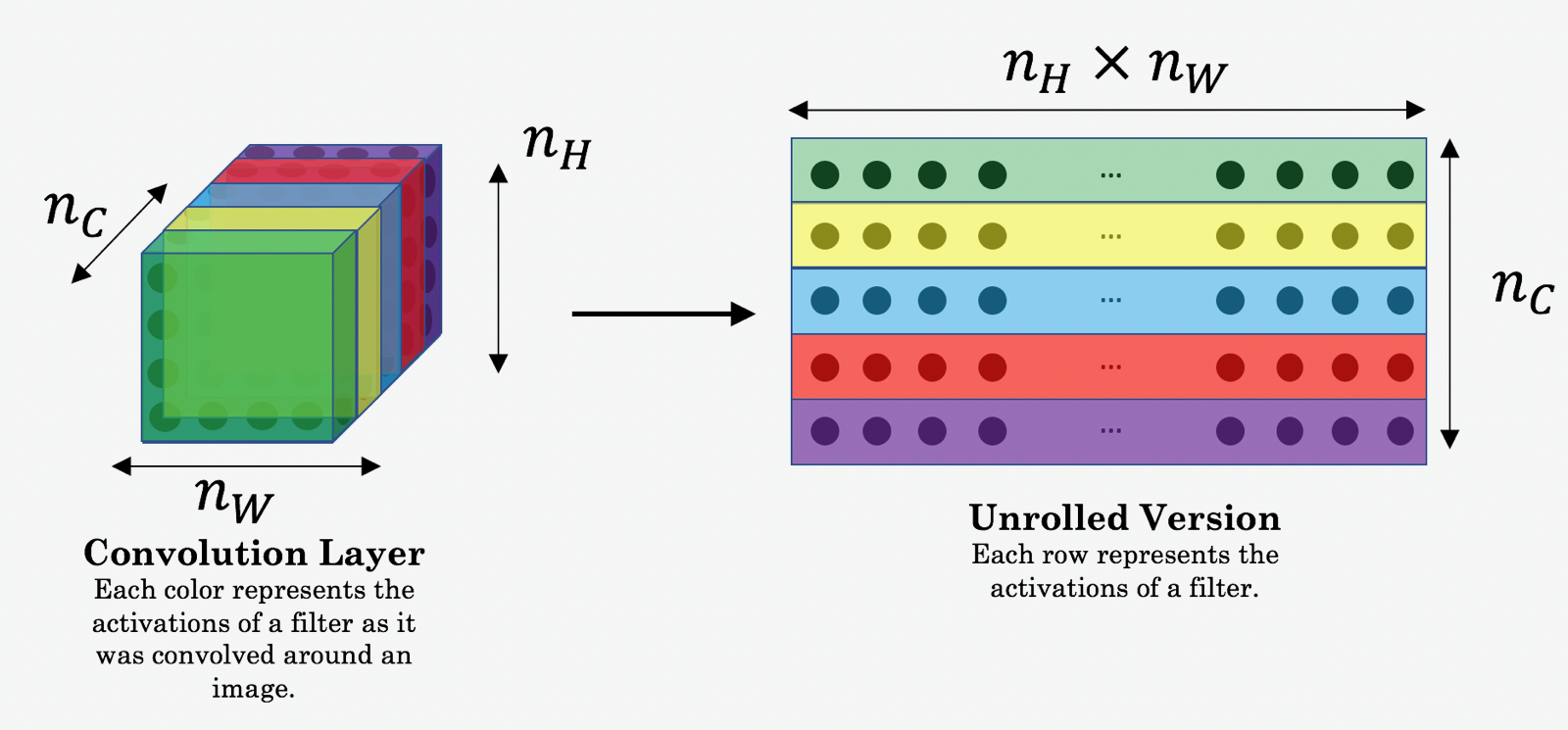
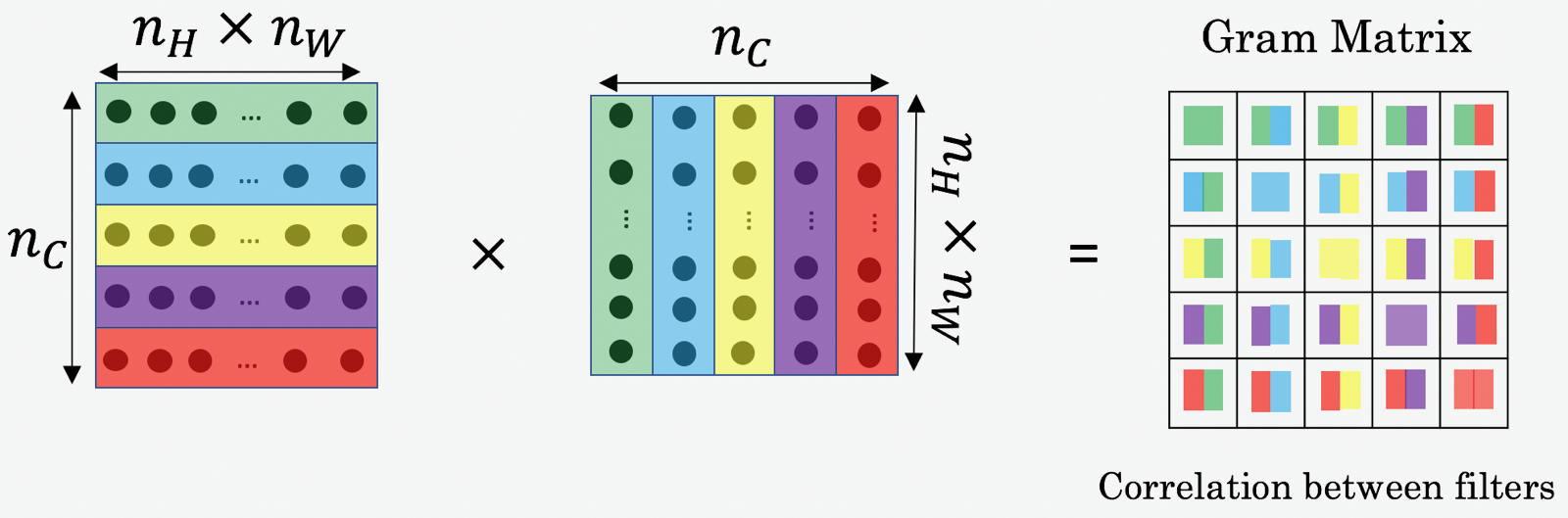
1 - Problem Statement¶
Neural Style Transfer (NST) is one of the most fun techniques in deep learning. As seen below, it merges two images, namely: a "content" image (C) and a "style" image (S), to create a "generated" image (G).
The generated image G combines the "content" of the image C with the "style" of image S.
In this example, you are going to generate an image of the Louvre museum in Paris (content image C), mixed with a painting by Claude Monet, a leader of the impressionist movement (style image S).

Let's see how you can do this.